Cuántos tipos de logaritmos existen

Tipos de logaritmos:

El concepto de logaritmo está directamente asociado a la Matemática. Se trata, de acuerdo a la teoría, del exponente al cual se necesita elevar una cierta cantidad positiva a fin de obtener un número específico. 

El logaritmo neperiano:

El término logaritmo neperiano suele referirse informalmente al logaritmo natural, aunque esencialmente son conceptos distintos. Para más detalles véase logaritmo natural.

En matemáticas, el logaritmo neperiano fue definido por primera vez por Leibniz dentro de una carta que remitió a Huygens en 1690, (en la cual usaba la notación b en lugar de e). No obstante, ya en 1618, en un apéndice de la obra de John Napier sobre logaritmos, aparecen calculados los logaritmos naturales de varios números. Sin embargo, en esa fecha la forma en que se conceptualizaban y calculaban los logaritmos no incluía el concepto de base e. La notación con base e, empezó a utilizarse a partir de los trabajos de Euler en 1731.

En términos de logaritmos modernos el logaritmo neperiano es la función dada como:

${\displaystyle \mathrm {NapLog} (x)={\frac {\log {\frac {10^{7}}{x}}}{\log {\frac {10^{7}}{10^{7}-1}}}}.}$

Puesto que es un cociente de logaritmos, la base del logaritmo escogido es irrelevante. No es, pues, un logaritmo en ninguna base particular en el sentido moderno del término.

Puede ser reescrito como:

${\displaystyle \mathrm {NapLog} (x)=\log _{\frac {10^{7}}{10^{7}-1}}10^{7}-\log _{\frac {10^{7}}{10^{7}-1}}x}$

logaritmo natural:

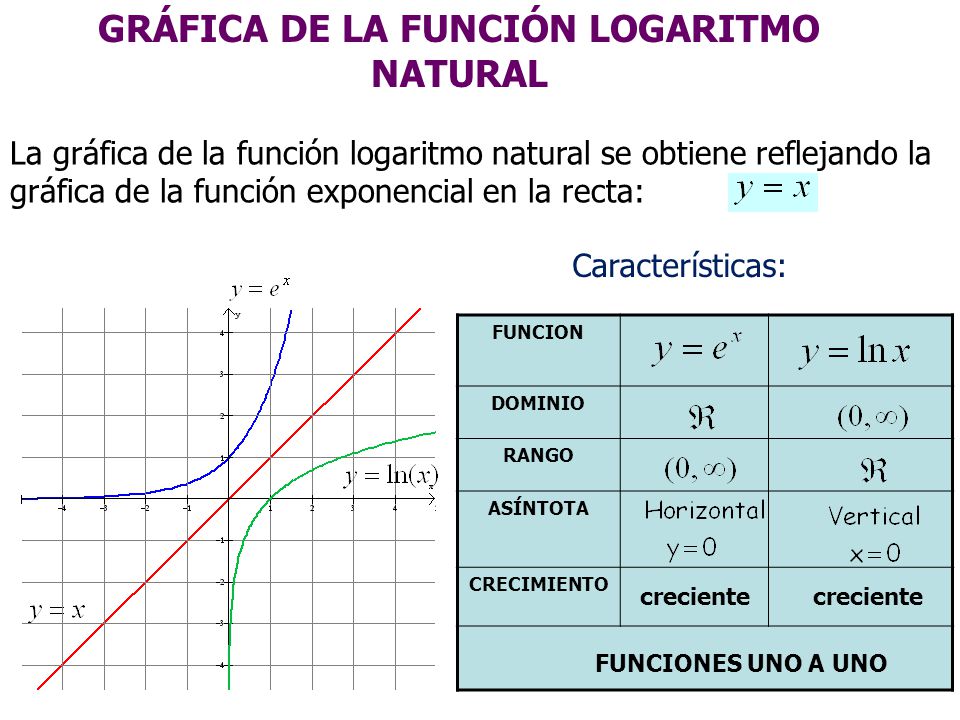
El logaritmo natural suele ser conocido como logaritmo neperiano, aunque esencialmente son conceptos distintos. Para más detalles, véase logaritmo neperiano.

En matemáticas se denomina logaritmo natural o logaritmo neperiano al logaritmo cuya base es el número e, un número irracional cuyo valor aproximado es 2,7182818284590452353602874713527. El logaritmo natural notado como ln(x), como log_e(x) y en algunos contextos como log(x), porque para ese número se cumple la propiedad de que el logaritmo vale 1.

El logaritmo natural de un número x es entonces el exponente a al que debe ser elevado el número e para obtener x. Por ejemplo, el logaritmo de 7,38905... es 2, ya que e²=7,38905... El logaritmo natural de e es 1, ya que e¹=e.

El logaritmo natural es una función real con dominio de definición los números reales positivos:

${\displaystyle {\text{ln}}:\mathbb {R} ^{+}\to \mathbb {R} }$

y corresponde a la función inversa de la función exponencial natural:

${\displaystyle e^{{\text{ln}}\,x}=x{\text{, para todo }}x>0}$

${\displaystyle {\text{ln}}(e^{x})=x\!}$

logaritmo decimal:

En matemáticas, se denomina logaritmo decimal, logaritmo común o logaritmo vulgar al logaritmocuya base es 10, por lo tanto, es el exponente al cual hay que elevar 10 (exponenciación) para obtener dicho número. Se suele denotar como log₁₀(x), o a veces como log(x), aunque esta última notación causa ambigüedades, ya que los matemáticos usan ese término para referirse al logaritmo complejo. El logaritmo decimal fue desarrollado por Henry Briggs.

                       

logaritmo binario:

En matemática el logaritmo binario o logaritmo en base 2: ${\displaystyle y=\log _{2}(x)}$ es la función matemática que determina a que valor yhay que elevarse a 2 para obtener x, es un caso particular de logaritmos en el que la base es 2.
Esta base tiene su importancia en informática (donde se lo representa comúnmente como lg n, o ld n que proviene del Latínlogarithmus dualis), dada la codificación binaria que se utiliza. Así por ejemplo con un número determinado de bits, ocho por ejemplo, se puede codificar una cantidad de información equivalente a ${\displaystyle 2^{8}=256}$, que es el número de variaciones que se pueden realizar con 0 y 1 en ocho posiciones. El uso del logaritmo binario, es útil cuando la información a calcular es la contraria: cuantas posiciones binarias y se necesitarán si se tiene que codificar x datos, direcciones, etc.