Ejercicios pdf

Ejercicios de LA PARÁBOLA E HIPÉRBOLA

LA PARÁBOLA

                                                            LA HIPÉRBOLA

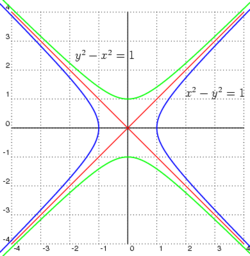
HIPÉRBOLA

Dados dos puntos $F_1$ y $F_2$ llamados focos, se denomina hipérbola al conjunto de puntos del plano tales que el valor absoluto de la diferencia de sus distancias a los focos es constante.

Ecuación canónica de la hipérbola

Con una deducción similar a la de la elipse, se obtiene:

  $$\frac{x^2}{a^2}–\frac{y^2}{b^2}=1$$

Es la ecuación canónica de la hipérbola con centro en $\left(0,0\right)$ y eje focal $y=0$ (eje $x$)

Elementos de la hipérbola

$$\frac{x^2}{a^2}–\frac{y^2}{b^2}=1$$

a se denomina semieje real o transverso

b se denomina semieje imaginario

2c es la distancia entre los focos

Ecuación ordinaria de la hipérbola (Centro fuera del origen)

La ecuación ordinaria de la hipérbola con centro en (h, k) con eje transversal

Horizontal es

y la ecuación ordinaria de la hipérbola con centro en (h,k) con eje transversal  vertical es :

https://es.scribd.com/document/270086311/Ecuacion-Ordinaria-de-La-Hiperbola

Ecuaciones de la hipérbola:

Ecuaciones canónicas en coordenadas cartesianas

La hipérbola cuyo centro se halla en el origen de coordenadas ${\displaystyle O(0,0)\,}$es representable mediante una de las siguientes ecuaciones denominadas de manera común como ecuación canónica o forma normal de la ecuación de una hipérbola:

(1)${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1\Rightarrow b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}}$

o

(2)${\displaystyle {\frac {y^{2}}{a^{2}}}-{\frac {x^{2}}{b^{2}}}=1\Rightarrow b^{2}y^{2}-a^{2}x^{2}=a^{2}b^{2}}$

En dichas ecuaciones ${\displaystyle a}$, ${\displaystyle b}$ y ${\displaystyle c}$, representan a los semiejes tranverso, conjugado y focal, respectivamente. La ecuación  representa a las hipérbolas cuyo eje focal es colineal al eje ${\displaystyle x}$ y para aquellas que lo son respecto al eje ${\displaystyle y}$. En la primera ecuación, los focos están en ${\displaystyle F(\pm c,0)}$ y los vértices en ${\displaystyle V(\pm a,0)}$. En la segunda, los focos están en ${\displaystyle F(0,\pm c)}$ y los vértices en ${\displaystyle V(0,\pm a)}$. En cualquier caso, la relación entre los tres semiejes viene dada por la igualdad:

        

Ecuaciones de una hipérbola con centro en el punto ${\displaystyle C(h,k)}$

Como en el caso anterior, la ecuación asume una de las siguientes formas:

${\displaystyle {\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1}$

${\displaystyle {\frac {(y-k)^{2}}{b^{2}}}-{\frac {(x-h)^{2}}{a^{2}}}=1}$

Ecuaciones en coordenadas polares[editar]

Dos hipérbolas y sus asíntotas en coordenadas cartesianas.

Hipérbola abierta de derecha a izquierda: 

${\displaystyle r^{2}=a\sec 2\theta \,}$

Hipérbola abierta de arriba abajo:

${\displaystyle r^{2}=-a\sec 2\theta \,}$

Hipérbola abierta de noreste a suroeste: 

${\displaystyle r^{2}=a\csc 2\theta \,}$

Hipérbola abierta de noroeste a sureste:

${\displaystyle r^{2}=-a\csc 2\theta \,}$

Hipérbola con origen en el foco derecho:

${\displaystyle r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1-\varepsilon \cos \theta }}}$

Hipérbola con origen en el foco izquierdo:

${\displaystyle r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1+\varepsilon \cos \theta }}}$

Ecuaciones paramétricas[editar]

Hipérbola abierta de derecha a izquierda:

${\displaystyle {\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=\pm a\cosh t+h\\y=b\sinh t+k\\\end{matrix}}}$

Hipérbola abierta de arriba abajo:

${\displaystyle {\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=a\sinh t+h\\y=\pm b\cosh t+k\\\end{matrix}}}$

En todas las fórmulas ${\displaystyle h}$ y ${\displaystyle k}$ son las abcisa y ordenada, respectivamente, del centro de la hipérbola, ${\displaystyle a}$ es la longitud del semieje mayor, ${\displaystyle b}$ es la longitud del semieje menor.

Parámetros focales de la hipérbola y=1/x[editar]

Correspondencia entre la hipérbola equilátera ${\displaystyle y=1/x}$ y su forma focal ${\displaystyle x'^{2}/2-y'^{2}/2=1}$

Para determinar los parámetros focales de una hipérbola equilátera definida según la ecuación:

${\displaystyle y=1/x}$

se puede aplicar una operación matricial que permite modificar las coordenadas de un conjunto de puntos del plano cuando se les aplica un giro ${\displaystyle \theta }$:

${\displaystyle {\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}}$

Como la hipérbola equilátera ${\displaystyle y=1/x}$ está girada con respecto al eje x según un ángulo ${\displaystyle \theta =45{\text{°}}}$, la matriz de transformación toma la forma:

${\displaystyle {\begin{bmatrix}x'\\y'\end{bmatrix}}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\-{\sqrt {2}}/2&{\sqrt {2}}/2\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}}$

https://es.wikipedia.org/wiki/Hip%C3%A9rbola

Parábola

Podemos definir la parábola como los puntos pertenecientes a un plano que equidistan de una recta llamada directriz y de un punto llamado foco.

Para que nos entendamos, para toda parábola que existe en el mundo, hay una recta en su mismo plano llamada directriz, y un punto también en el mismo plano llamado foco, que tienen la propiedad de que cualquier punto perteneciente a la curva, se encuentra a la misma distancia tanto del foco como de la directriz.

Otro punto importante a tener en cuenta es el vértice, que es el punto de la parábola que se encuentra más cercano a la directriz. Si realizamos una recta perpendicular a la directriz que pase por el vértice, diremos que esa recta se llama eje de simetría de la parábola.

http://www.matematicasdigitales.com/la-parabola/

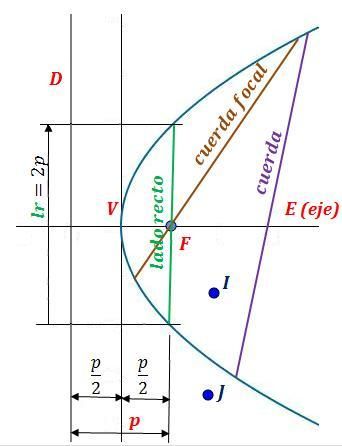
Los elementos de una parábola son:

• Foco: el foco F es el punto fijo. Los puntos de la parábolaequidistan del foco y la directriz.
• Directriz: es la recta fija D. Los puntos de la parábola equidistan de la directriz y el foco.
• Radio vector: es el segmento R que une el foco con cada uno de los puntos de la parábola. Es igual al segmento perpendicular a la directriz desde el punto correspondiente.
• Eje: es la recta E perpendicular a la directriz que pasa por el foco y el vértice. Es el eje de simetría de la parábola.

• Parámetro: es el vector p, que va desde el foco al punto más próximo de la directriz.
  Es importante el signo del parámetro. En las parábolas verticales, cuando el parámetro es positivo la parábola se abre hacia arriba. Cuando pes negativo, la parábola se abre hacia abajo. Igualmente, en las parábolashorizontales, cuando p es positivo, se abre hacia la derecha y cuando p es negativo, la parábola se abre a la izquierda.
• Vértice: es el punto V de la intersección del eje y la parábola.
• Distancia focal: distancia entre el foco F y el vértice V. Es igual a p/2.
• Puntos interiores y exteriores: la parábola divide el plano en dos regiones. Los puntos que están en la región del foco se llaman puntos interiores (I), mientras que los otros son los exteriores (J).
• Cuerda: segmento que une dos puntos cualesquiera de la parábola.
• Cuerda focal: una cuerda que pasa por el foco F.
• Lado recto: Cuerda focal paralela a la directriz D y, por tanto, perpendicular al eje E. Su longitud es dos veces el parámetro (2p, pues se ven en la figura dos cuadrados unidos iguales de lado p).

https://www.universoformulas.com/matematicas/geometria/elementos-parabola/         

FORMAS DE LA ECUACIÓN DE LA PÁRABOLA:

FORMA CANÓNICA DE LA PARÁBOLA:



El vértice de la parábola coincide con el origen de coordenadas.



https://www.google.com.pe/search?q=forma+canonica&source=lnms&tbm=isch&sa=X&ved=0ahUKEwit5vq64_jeAhXFzlMKHWNyC0AQ_AUIDigB&biw=1366&bih=626#imgrc=zr8Y7ovnxuqaXM: